The Fraud of Rationality and the Practical Limits of Reason

How can anyone criticize reason? How could reason anything other than a force for good? The modern world is so deeply invested in the supremacy of reason and scientific empiricism that challenging the efficacy and good of either is a new kind of heresy. Yet reason does have its limitations, both in practice and in theory. The work of computer scientists and mathematicians in the 20th century have critically undermined reason as a chief means of knowing truth.

Generally speaking, reason refers to deductive logic. Aristotle (384 – 322 BC) is the first person credited to formally studying logic but it was his student Theophrastus (371 – 287 BC) to first describe “Modus Ponens,” that is, logical inference from general rules. Deductive logic is the process of correctly applying general rules to specific facts to produce a conclusion. The famous example of “Modus Ponens” is that given the fact “Socrates is a man” and the rule “all men are mortal” the logical inference is that “Socrates is mortal.” Logical deduction reasons from a premise to a conclusion through the application of rules i.e. inference. More generally, logic can be defined as any process of reasoning that produces true conclusions given correct information.

Naturally, multiple rules can be “chained” together, that is, the conclusion of one inference becomes the premise of the next. For example, consider the rules “all men must eat” and “all who eat are mortal” along with the fact that “Socrates is a man.” By applying the first rule the conclusion is “Socrates must eat.” This conclusion is a new fact, a fact inferred by logic. This fact is just as reliable as the given fact of “Socrates is a man” and can be used for further inference. Hence the second rule “all who eat are mortals” is applied to “Socrates must eat” to infer that “Socrates is mortal.” This is the heart of logical deduction, given some facts or assumptions and some general rules, inference is applied to produce new facts, then the process is repeated until there is either nothing left to conclude or until a conclusion is reached that answers a relevant question e.g. “Is Socrates mortal?”

In general, inference is much more challenging than this example with only one fact and two rules. The difficulty is in determining which rules to apply and to which facts. Consider this example.

Facts:

Socrates is a man.

A horse is a beast.

Rules:

1. All beasts are living things.

2. All men are living things.

3. All living things must eat.

4. All who eat are mortal.

5. All who make money pay taxes.

6. All men must make money.

For the sake of the example, leave aside friends, family members, and others who in reality define rule #6. These rules and facts can be used to infer an answer to the question “Does Socrates pay taxes?” Starting with the fact, “Socrates is a man” the rules produce two “chains” of inference, i.e. rules #2, #3, and #4 applied in that order, concluding that “Socrates is mortal” and rules #5, #6 applied in that order concluding that “Socrates plays taxes.” The trouble is that the process of inference does not know which chain to follow to reach the relevant, ultimate conclusion that answers the question. In this example, only one “chain” is useful to finding the answer and the other is a waste of effort. The existence of multiple chains of inference is called “branching.” The process of inference is analogous to the shape of a tree with the starting facts at the “root,” the different chains of inference forming branches, and the ultimate conclusions being “leafs.”

This illustrates the first major problem with logical deduction, the number of possible conclusions grows rapidly as the number of facts and rules considered increases. Continuing with the example, consider the question “Does a horse pay taxes?” For this question, there is one valid chain of inference using rules #1, #3, and #4 but its conclusion, “a horse is mortal” is not relevant. Strictly speaking, the question cannot be answered unless it is assumed that statements without a supporting chain of inference are false. If that assumption is made, inference must be performed to determine all true conclusions before negative (false) conclusions can be made. In the analogy of the tree, starting at the root, logical deduction must make its way to each leaf to be certain about its conclusions.

In the twentieth century, mathematicians, logicians, and computer scientists formalized and systematized deductive logic into a problem that can be algorithmically solved by a computer. The problem is called “Satisfibility” or “SAT” for short. The formalized problem SAT is a bit different from the “tree” of inference previous described but the effect is the same. The problem is given a collection of facts or assumptions that are either true or false and some general rules, can answer to a true or false question be found. A question is “satisfied” if there is a chain of inference from the given facts to a relevant conclusion. An algorithm is a step-by-step systematic procedure that solves a particular type of problem and is generally performed by a computer. There are many algorithms that solve the “SAT” problem, that is, perform logical inference on a set of facts and rules. However, all of them are variations on simply exhaustively exploring the “tree” of possible inferences and conclusions.

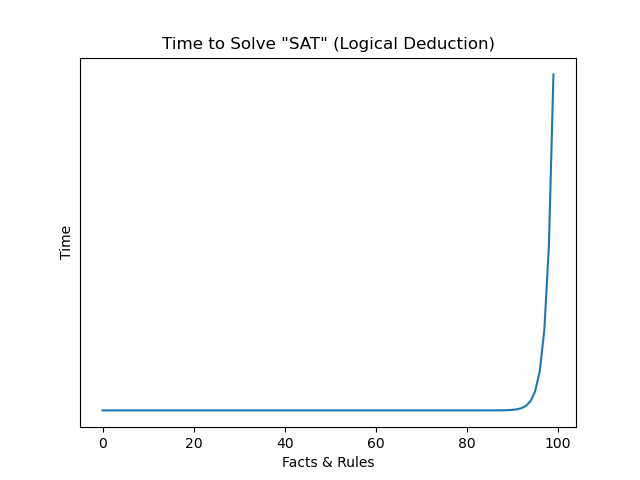
What this means is that computers can solve any logical deduction problem. However, the catch is the amount of time it takes to solve these problems. In general, the “tree” of inference is huge and is characterized by an exponential number of possible inferences and conclusions. If the number of facts and rules being considered is n then the number of possible inferences and conclusions is about 2^n (exponential). This means smaller examples like ones earlier presented are solvable by a human or computer in a reasonable amount of time because they consist of only a handful of facts and rules. However for other examples involving thousands of facts and rules, there simply is not enough time to consider all the possible inferences. There is a “wall” of which beyond a certain size, there simply is not enough time to find an answer.

In other words, correct facts and rules are put into a computer program, the program starts running and it never stops. An answer exists but there is simply no way to find it in a reasonable amount of time. This is what computer scientists refer to as “computational intractability.” You may have experienced computational intractability first-hand if you have played chess. When considering your move, you should consider all the possible counter-moves your opponent may make. To understand if their counter-move is a problem for you, you need to consider which moves you can make to counter their counter and so on and so forth. The enormous number of possible moves, counters, and counters to the counters etc is mind boggling. The “SAT” problem is a needle in a haystack scenario where the needle is the answer and the haystack is the time until the sun goes nova.

Further, despite computers generally getting faster year after year, their pace of improvement is not fast enough to be relevant to large examples of “SAT.” Likewise, quantum computing can help, but it too cannot keep up with the exponential amount of time required to solve the problem in general. While the computer science community has been able to observe computational intractability, it is unable to definitively prove that the “SAT” problem and other similar difficult problems will never have an algorithm that allows the problem be solved in a reasonable amount of time. However, what the community does know is that a breakthrough that would allow “SAT” to be solved in a reasonable amount of time would have radical and very unrealistic implications. The implications would be as bizarre and unexpected as physics discovering anti-gravity or time-travel.

Besides the limitation of time, logic also suffers from the issue of brittleness. Logical always produces correct answers given correct facts, however if the initial “facts” are wrong then whatever conclusions are deduced cannot be trusted. One incorrect “fact” will poison the conclusions so badly it is possible that inference will yield a conclusion that is the exact opposite of the truth. This is what computer scientists call the “garbage in, garbage out” problem. Logical deduction has no means of self-correction. The result of inference with bad “facts” can be contradictory conclusions and this may not be evident until the “tree” of inference is quite large and a lot of effort has been expended. The same brittleness applies to rules used to make deductions as well. A single erroneous rule can result in a wrong conclusion even with correct “facts.”

In the early days of artificial intelligence (AI) research, 1950’s through 1970’s, AI systems were almost exclusively logical deduction systems in one form or another. The “garbage in, garbage out” problem plagued researchers when they tried applying their systems to the real world. Misperception, a failure to see, hear, or otherwise sense the world would result in erroneous “facts” being supplied to AI systems. The result was a lot of sophisticated, logical AI systems with no practical application. This problem hit its peak in the 1980’s which is often referred to as the “AI winter” since many AI research projects were abandoned for their lack of applicability. During this time machine learning, which is a branch of AI based on probability and statistics, gained traction since it is naturally more resistant to erroneous data.

In addition to erroneous “facts,” coming up with exact, logical rules is difficult for both people and computers. It may be tempting to think a rule such as “all men go bald” or “all birds fly” are logical when in fact they are only correct part of the time. For a rule to be logical it must be correct every time it is applicable. The rules that seem natural to people usually turn out to be mostly correct, rules of thumb rather than exact logical rules.

These limitations of logic fundamentally undermine all worldviews based on Rationalism. Logic needs a starting point, principles or facts upon which to reason. However, determining the correct principles or facts cannot be done logically and a single mistake potentially undermines all of its conclusions. Further, logic alone cannot confirm that the principles or “facts” initially assumed are correct, since using a conclusion to justify a premise is the definition of circular reasoning. Even if the correct principles and/or facts were known, there would still be truth beyond the horizon of proof due to the general intractability of logical deduction. A Rationalist worldview is therefore brittle and limited, and must acknowledge that there is truth that will always remain a mystery. In other words, Rationalist worldviews are neutered to the point of uselessness.

Still logic deduction remains useful despite it being limited by its initial assumptions and by its intractability. Logic works in the “middle ground” between first principles and the horizon of what is knowable. Since first principles or “facts” are so critical, a robust worldview would use principles that best match reality and have supported human life for a long time and are associated with human flourishing. It is rational and reasonable to look to religion and tradition as a source of reliable well-trusted principles. The values of religions and traditions are tested in the lives of the individuals who follow them and the best ones are those that have stood the test of time. Religions and traditions that lasted millennia and have led to human flourishing are most likely to be grounded in principles that best reflect reality. 

In the end, as useful as logic is, it is severely limited. Complexity and time create a horizon that logic cannot see beyond. Further, logic cannot supply the first principles it is completely dependent upon. These flaws mean Rationalism is not a reliable guide for human life and people should look to worldviews that have stood the test of time.